Human SLAM

Indoor Localisation of Devices and Users

IEEE International Conference on Internet-of-Things Design and Implementation
Berlin, 2016


Wouter Bulten

Artificial Intelligence Department
Radboud University, Netherlands

In collaboration with:

Anne van Rossum (DoBots & Almende) & Pim Haselager (Donders Institute)

Supported by the Proheal project (n. 12007)
funded by Information Technology for European Advancement (ITEA2)

In a smart home / hospital / office, how do we act when..


We do not know where users are?


Location is key in smart spaces

What can we do without locations of devices?


Relative position vs absolute

We need both the user and the system

But, we can benefit from this combination

Problem statement


Given an unknown building with (smart) devices, can we autonomoumsly locate these devices and the users that walk around inside the building?

Requirements

No prior configuration or hardware
Cost-effective, resilliant to changes, easy to deploy
Protect privacy
Increase user adoption
Realtime
Localisation must be instant

Outline

Robotics:  FastSLAM & Particle Filters

Sources of Input:  What can we use?

The result:  Demo & real world findings

The world of Indoor Localisation

Lets talk about robots..

Simulteneous Localisation and Mapping (SLAM)

Given robot's controls and sensor readings what is the current estimated location and map of the environment?


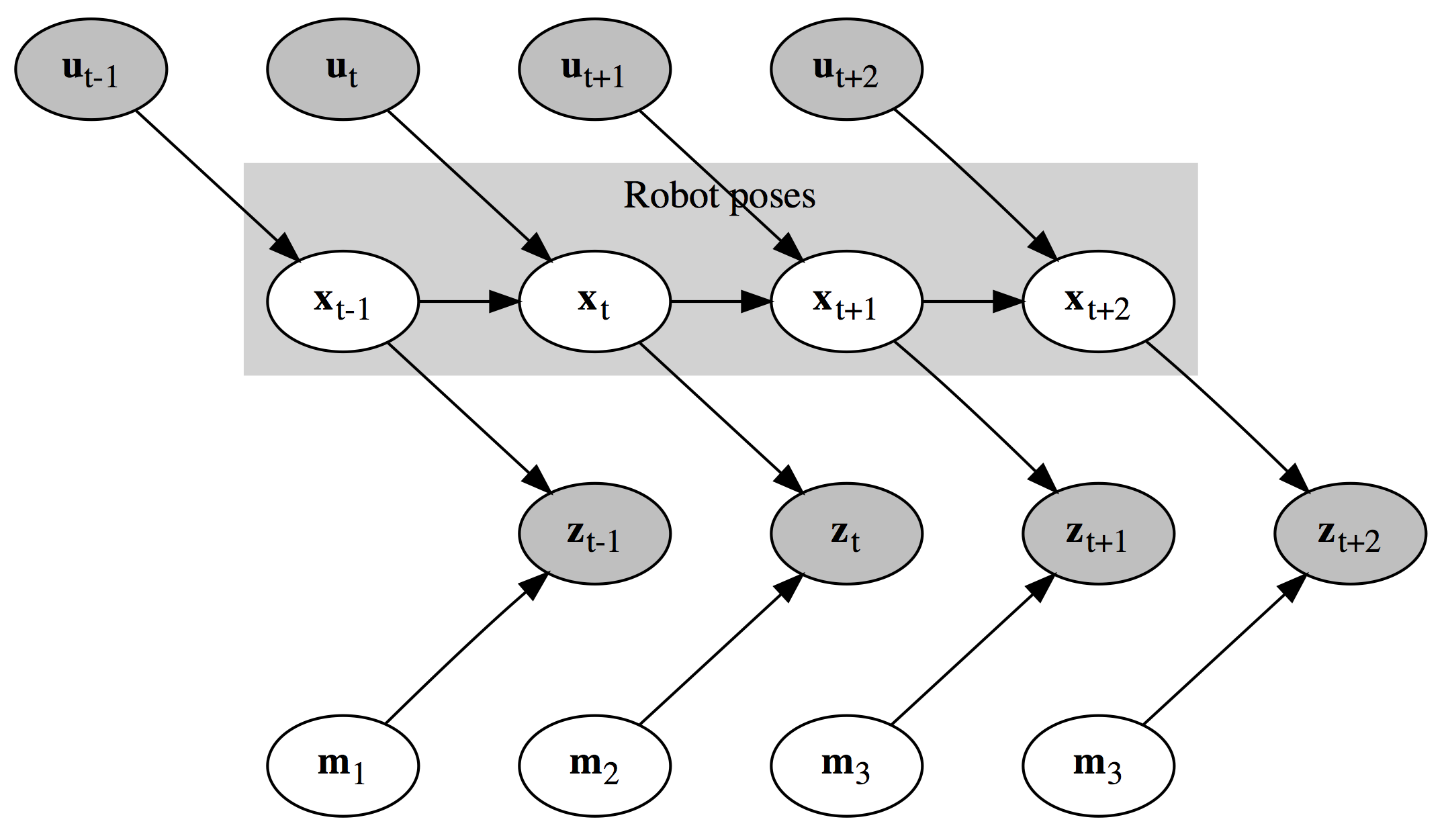
FastSLAM

Online algorithm for solving the SLAM problem


Given observations and the controls, what is the robot's position on the current map?

$$ p(x_{0:t}, m_{1:M} | z_{1:t}, u_{1:t}) $$


Independent landmarks

Uses Rao-Blackwellized particle filter for estimation

$$ p(x_{0:t}, m_{1:M} | z_{1:t}, u_{1:t}) = p(x_{0:t} | z_{1:t}, u_{1:t})\; \prod_{i=1}^M p(m_i | x_{0:t}, z_{1:t}) $$

Robot's sensor readings → ?

Devices are often connected wirelessly

In our case: Bluetooth Low Energy (BLE)


→ Received Signal Strength Indicator (RSSI)

Measured RSSI

Beacon at fixed distances to the receiver with clear line of sight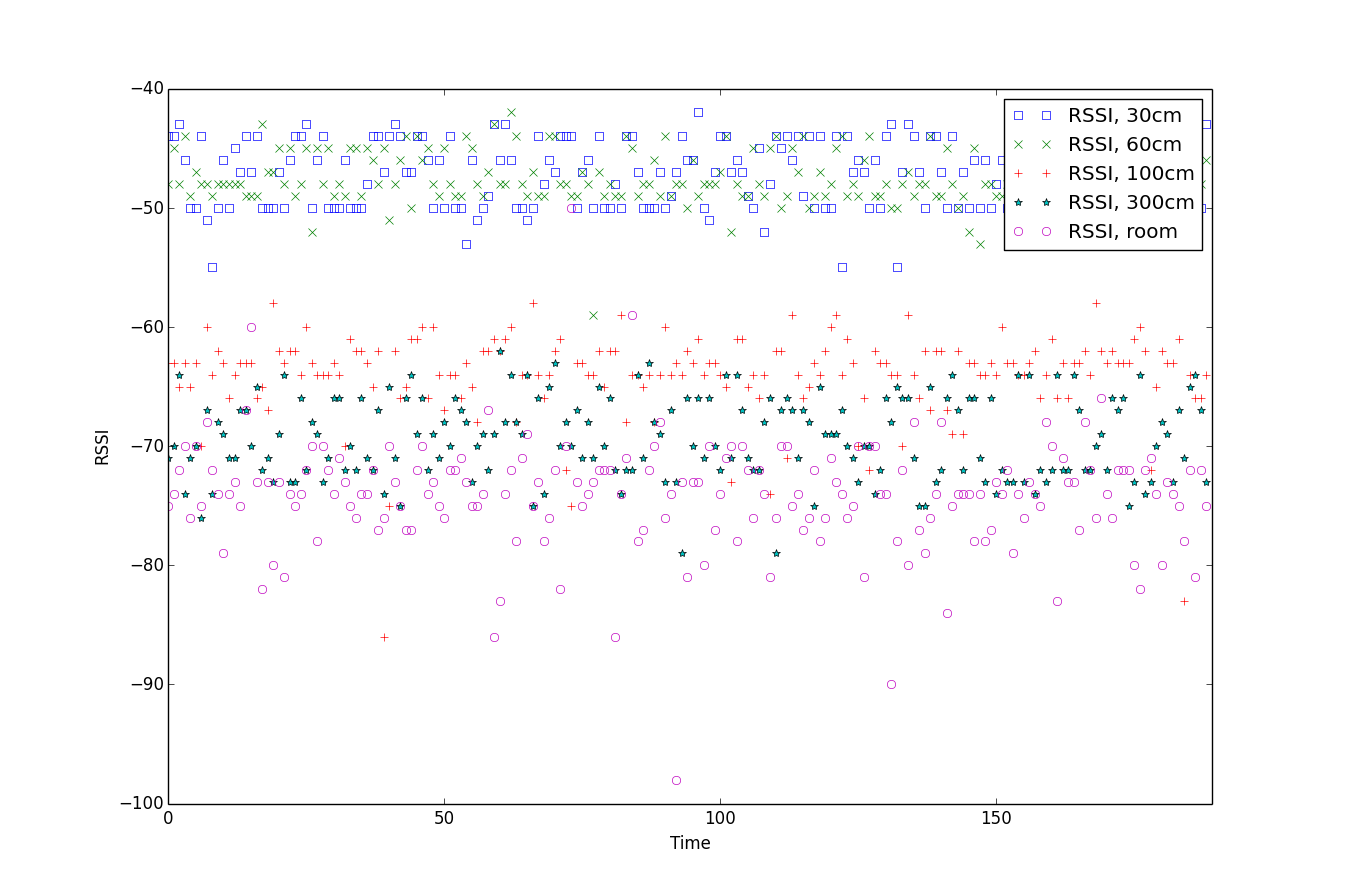

Log-distance path loss model:


$$RSSI = -10n \log_{10}(\frac{d}{d_{0}}) + A$$

  • $d$ the distance to the device
  • $A$ signal strength at $d_0$
  • $n$ an evironment constant

Estimated distance

Beacon at fixed distances to the receiver with clear line of sight

Is RSSI usefull?

High levels of noise due to:

  • Walls, humans, objects
  • Multi-path reflections
  • Radio differences


However, available in almost any consumer device
and filtering can help!

Filtered RSSI signal

Using a Kalman filter with static motion model
$$ x_{t} = A_{t}x_{t-1} + B_{t}u_{t} + \epsilon_{t} $$ $$ z_{t} = C_{t}x_{t} + \delta_{t} $$
$$\bar\mu_t = A_t \mu_{t-1} + B_t u_t$$ $$\bar\Sigma_t = A_t \Sigma_{t-1} A_t^T + R_t$$
$$K_t = \bar\Sigma_t C_t^T (C_t \bar\Sigma_t C_t^T + Q_t)^{-1}$$
$$\mu_t = \bar\mu_t + K_t(z_t - C_t \bar\mu_t)$$ $$\Sigma_t = (I - K_t C_t) \bar\Sigma_t$$

Robot's control → ?

RSSI gives us distance, but distance needs a where


Users can ground the measurements


Accelerometer
Physical acceleration in $x, y, z$
Compass
Heading relative to global north

Simultaneous Localisation and Configuration (SLAC)

Signal strength as observation

Motion measurements as control


Particle filter at the core

Extended Kalman filters for refinement

$\bar\chi_t = \chi_t = \emptyset$

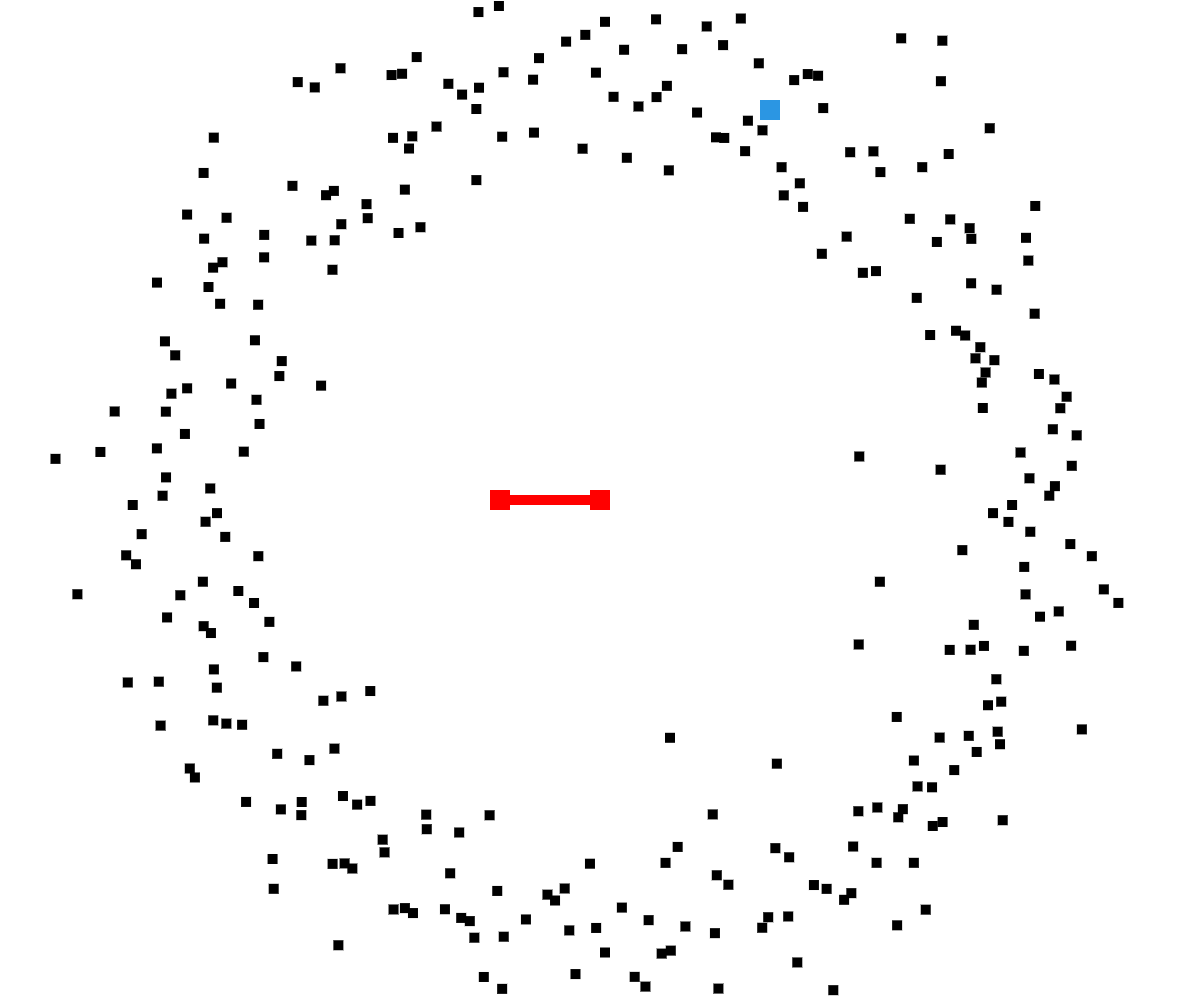
$\bar\chi_t = \chi_t = \emptyset$

Initialisation, for $m \in M$:

$x_t^{[m]} \sim p(x_t | z_t, x_t^u$)

$\bar\chi_t = \chi_t = \emptyset$

Initialisation, for $m \in M$:

$x_t^{[m]} \sim p(x_t | z_t, x_t^u$)

Sample step, for $m \in M$:

$x_t^{[m]} \sim p(x_t | u_t, x_{t-1}^{[m]}$)

$w_t^{[m]} = p(z_t | x_t^{[m]}) = \frac{1}{\sigma\sqrt{2\pi}} e^{-\frac{(z_t-\mu)^{2}}{2\sigma^{2}}}$

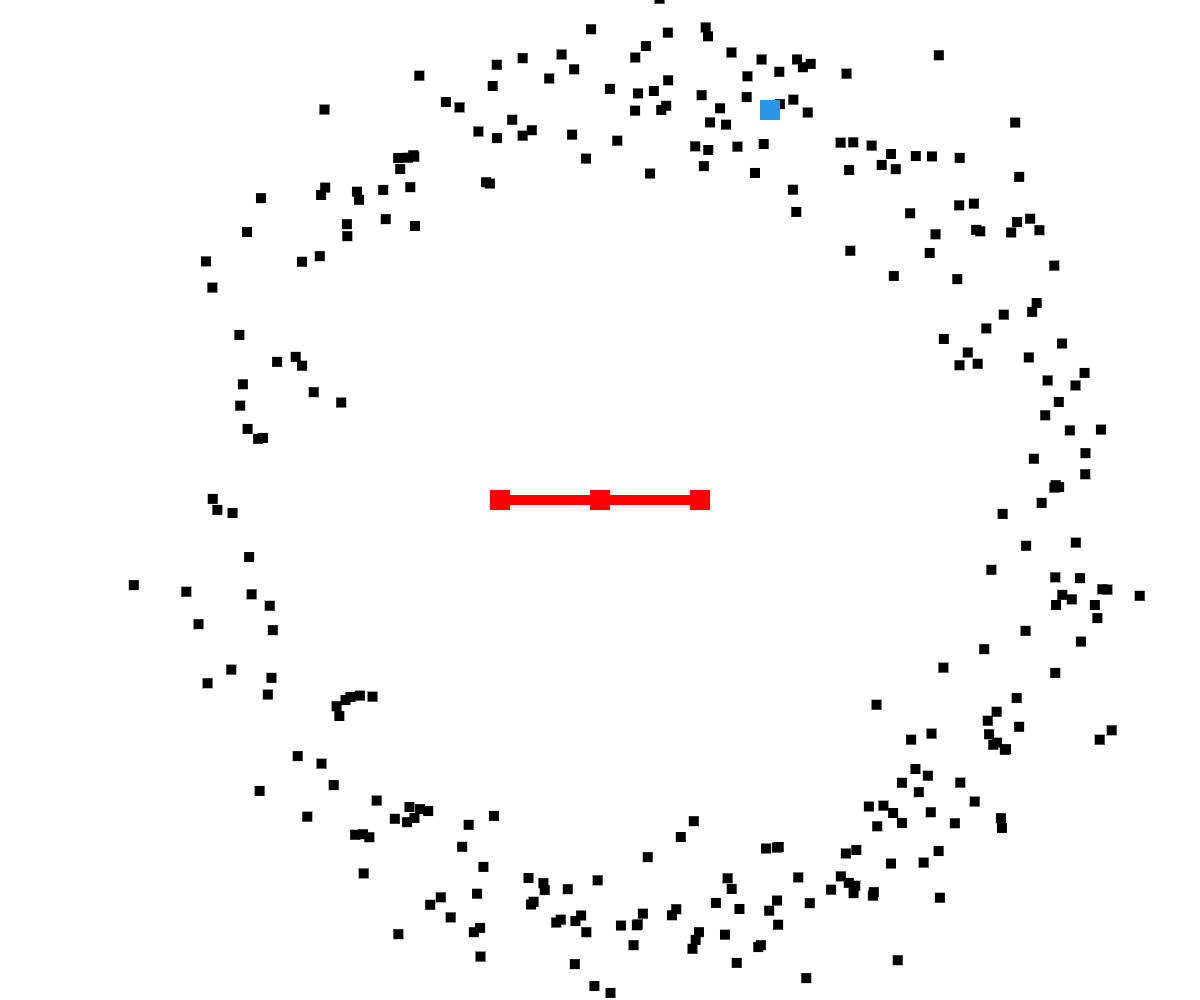
$\bar\chi_t = \chi_t = \emptyset$

Initialisation, for $m \in M$:

$x_t^{[m]} \sim p(x_t | z_t, x_t^u$)

Sample step, for $m \in M$:

$x_t^{[m]} \sim p(x_t | u_t, x_{t-1}^{[m]}$)

$w_t^{[m]} = p(z_t | x_t^{[m]}) = \frac{1}{\sigma\sqrt{2\pi}} e^{-\frac{(z_t-\mu)^{2}}{2\sigma^{2}}}$

Resample step, for $m \in M$:

draw $i$ with probability $\propto w_t^{[m]}$

$\chi_t = \chi_t + x_t^{[m]}$

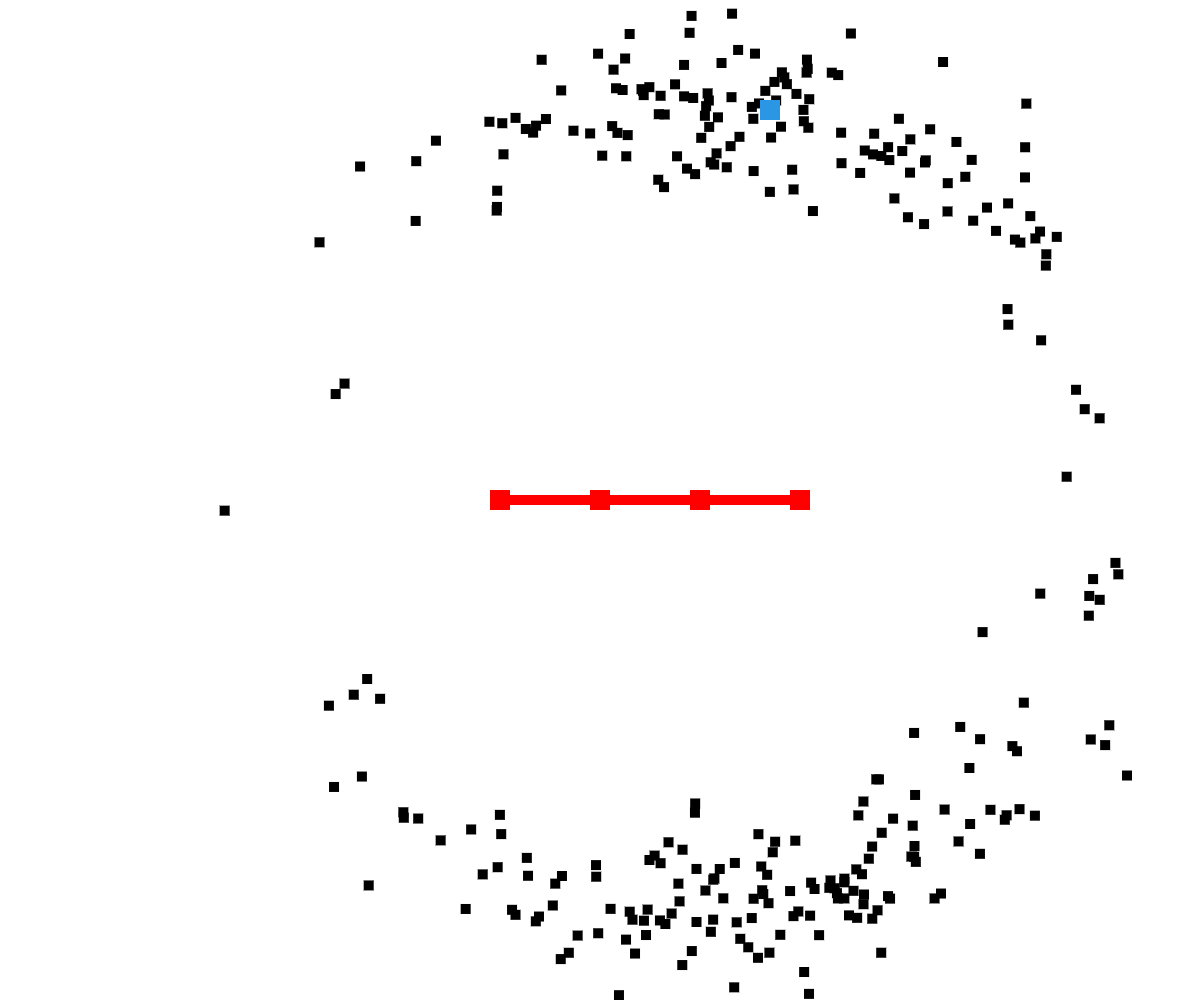
$\bar\chi_t = \chi_t = \emptyset$

Initialisation, for $m \in M$:

$x_t^{[m]} \sim p(x_t | z_t, x_t^u$)

Sample step, for $m \in M$:

$x_t^{[m]} \sim p(x_t | u_t, x_{t-1}^{[m]}$)

$w_t^{[m]} = p(z_t | x_t^{[m]}) = \frac{1}{\sigma\sqrt{2\pi}} e^{-\frac{(z_t-\mu)^{2}}{2\sigma^{2}}}$

Resample step, for $m \in M$:

draw $i$ with probability $\propto w_t^{[m]}$

$\chi_t = \chi_t + x_t^{[m]}$

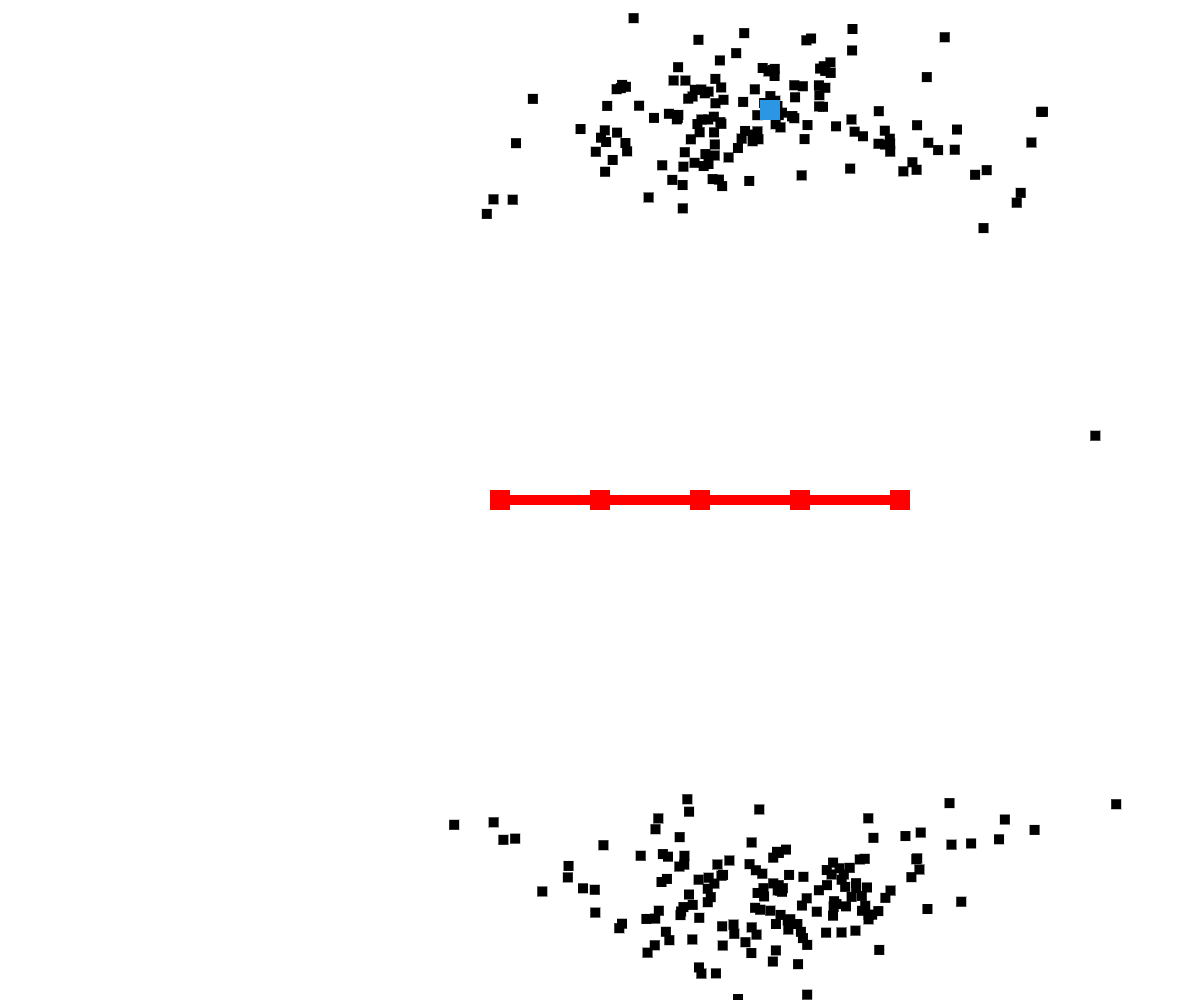
$\bar\chi_t = \chi_t = \emptyset$

Initialisation, for $m \in M$:

$x_t^{[m]} \sim p(x_t | z_t, x_t^u$)

Sample step, for $m \in M$:

$x_t^{[m]} \sim p(x_t | u_t, x_{t-1}^{[m]}$)

$w_t^{[m]} = p(z_t | x_t^{[m]}) = \frac{1}{\sigma\sqrt{2\pi}} e^{-\frac{(z_t-\mu)^{2}}{2\sigma^{2}}}$

Resample step, for $m \in M$:

draw $i$ with probability $\propto w_t^{[m]}$

$\chi_t = \chi_t + x_t^{[m]}$

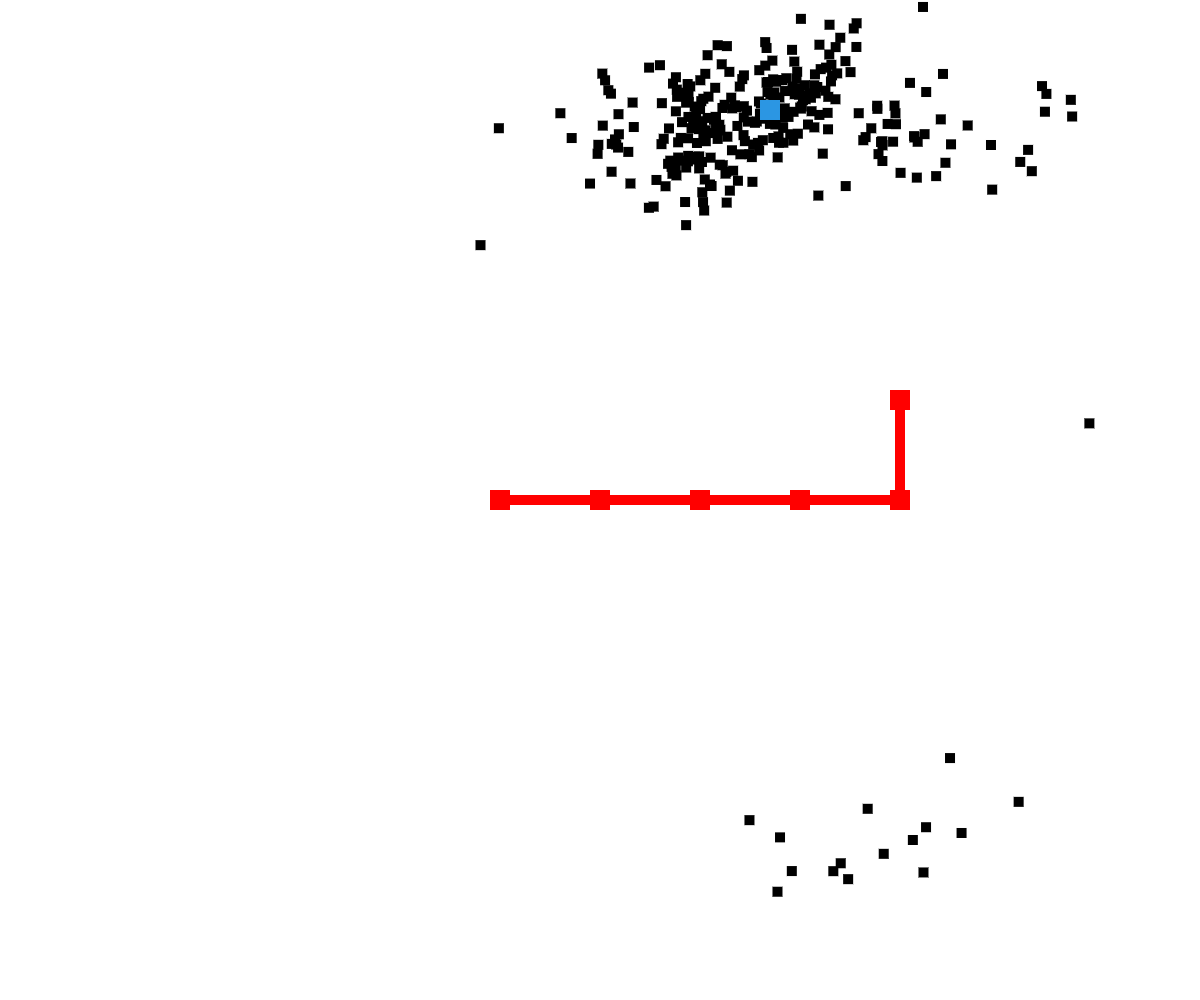
$\bar\chi_t = \chi_t = \emptyset$

Initialisation, for $m \in M$:

$x_t^{[m]} \sim p(x_t | z_t, x_t^u$)

Sample step, for $m \in M$:

$x_t^{[m]} \sim p(x_t | u_t, x_{t-1}^{[m]}$)

$w_t^{[m]} = p(z_t | x_t^{[m]}) = \frac{1}{\sigma\sqrt{2\pi}} e^{-\frac{(z_t-\mu)^{2}}{2\sigma^{2}}}$

Resample step, for $m \in M$:

draw $i$ with probability $\propto w_t^{[m]}$

$\chi_t = \chi_t + x_t^{[m]}$

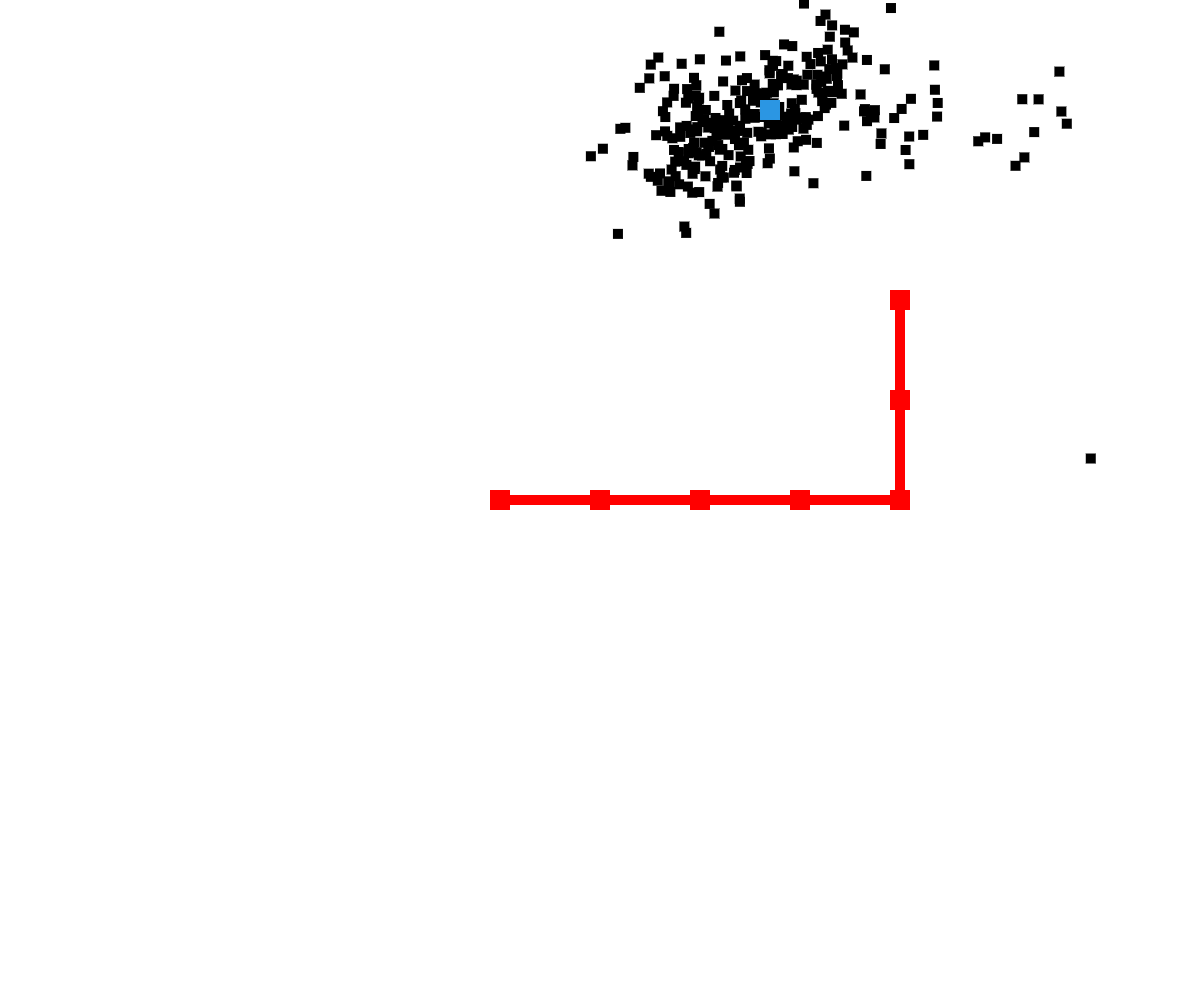
$\bar\chi_t = \chi_t = \emptyset$

Initialisation, for $m \in M$:

$x_t^{[m]} \sim p(x_t | z_t, x_t^u$)

Sample step, for $m \in M$:

$x_t^{[m]} \sim p(x_t | u_t, x_{t-1}^{[m]}$)

$w_t^{[m]} = p(z_t | x_t^{[m]}) = \frac{1}{\sigma\sqrt{2\pi}} e^{-\frac{(z_t-\mu)^{2}}{2\sigma^{2}}}$

Resample step, for $m \in M$:

draw $i$ with probability $\propto w_t^{[m]}$

$\chi_t = \chi_t + x_t^{[m]}$

Start
[Not supported by viewer]
Read RSSI & motion data
[Not supported by viewer]
New step?
[Not supported by viewer]
No
[Not supported by viewer]
Sample new pose
[Not supported by viewer]
Yes
[Not supported by viewer]
New 
landmark?
[Not supported by viewer]
Initialisation filter
[Not supported by viewer]
Update EKF
[Not supported by viewer]
No
[Not supported by viewer]
Yes
[Not supported by viewer]
Resample
[Not supported by viewer]
Estimate
ready?
[Not supported by viewer]
Init EKF
[Not supported by viewer]
Yes
[Not supported by viewer]
No
[Not supported by viewer]
For each particle
[Not supported by viewer]

Updating the filter

  1. Sample pose

    $$x_{t}^{[m]} \sim p(x_{t} | x_{t-1}^{[m]}, u_{t})$$

  2. Update EKF's

    $$[x_{t+1}^{[m]}, y_{t+1}^{[m]}]^T = [x_{t}^{[m]}, y_{t}^{[m]}]^T + Kv$$

    $$\Sigma_{t+1}^{[m]} = \Sigma_{t}^{[m]} - K \sigma_v K^T$$

  3. Resample

    $$w_{t}^{[m]} = w_{t-1}^{[m]} f(z | h_{m}, \sigma_z)$$

Particle representation:
$$Y_{t}^{[m]} =\Big\langle x_{t}^{[m]}, \langle\mu_{1,t}^{[m]}, \Sigma_{1,t}^{[m]}\rangle, \ldots, \langle\mu_{N,t}^{[m]}, \Sigma_{N,t}^{[m]} \rangle\Big\rangle$$

EKF Update

\begin{align} h_m(x_b^{[m]}, y_b^{[m]}) &= \sqrt[]{(x_{u,t}^{[m]} - x_b^{[m]})^2 + (y_{t,u}^{[m]} - y_b^{[m]})^2}\\ v &= z - h_m\\ H = \frac{\partial h_m}{\partial [x_b^{[m]} y_b^{[m]}]} &= [\frac{x_{u,t}^{[m]} - x_{b}^{[m]} }{h_m}, \frac{y_{u,t}^{[m]} - y_b^{[m]}}{h_m}]^T\\ \sigma_v &= H \Sigma_{b,t}^{[m]} H^T + Q_t\\ K &= \Sigma_{b,t}^{[m]} H^T \sigma_v^{-1} \end{align}

$$[x_{t+1}^{[m]}, y_{t+1}^{[m]}]^T = [x_{t}^{[m]}, y_{t}^{[m]}]^T + Kv$$

$$\Sigma_{t+1}^{[m]} = \Sigma_{t}^{[m]} - K \sigma_v K^T$$

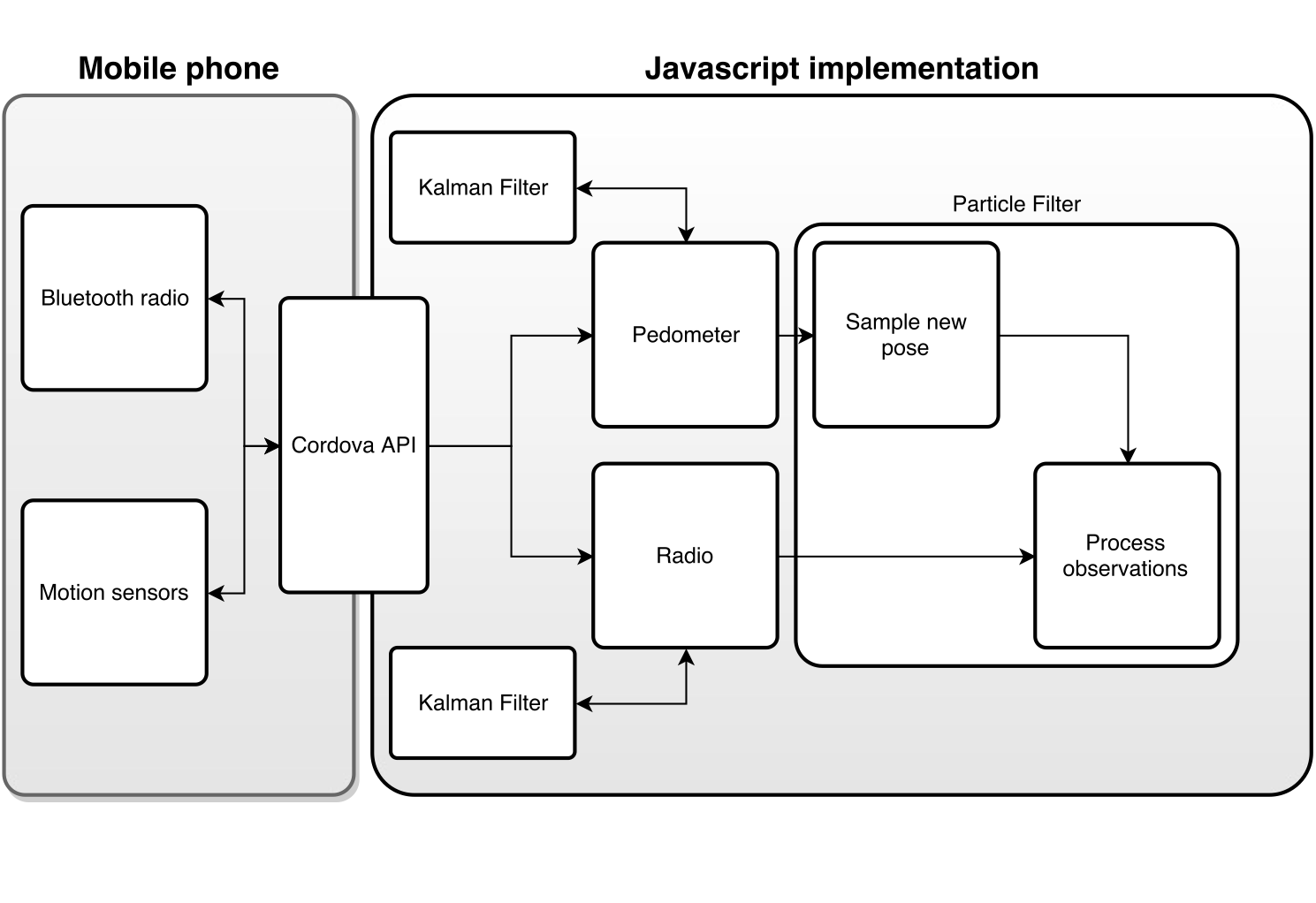
Implementation details

Fully written in Javascript
(including pedometer, SLAM algorithm, particle filters and visualisations)

ECMAScript 6/2015
(with BabelJS as transpiler)

Built for Android & iOS
(Using Cordova)

Bluetooth devices from DoBots
(iBeacon compatible, BLE)

Code on GitHub
(See: github.com/wouterbulten/slacjs)

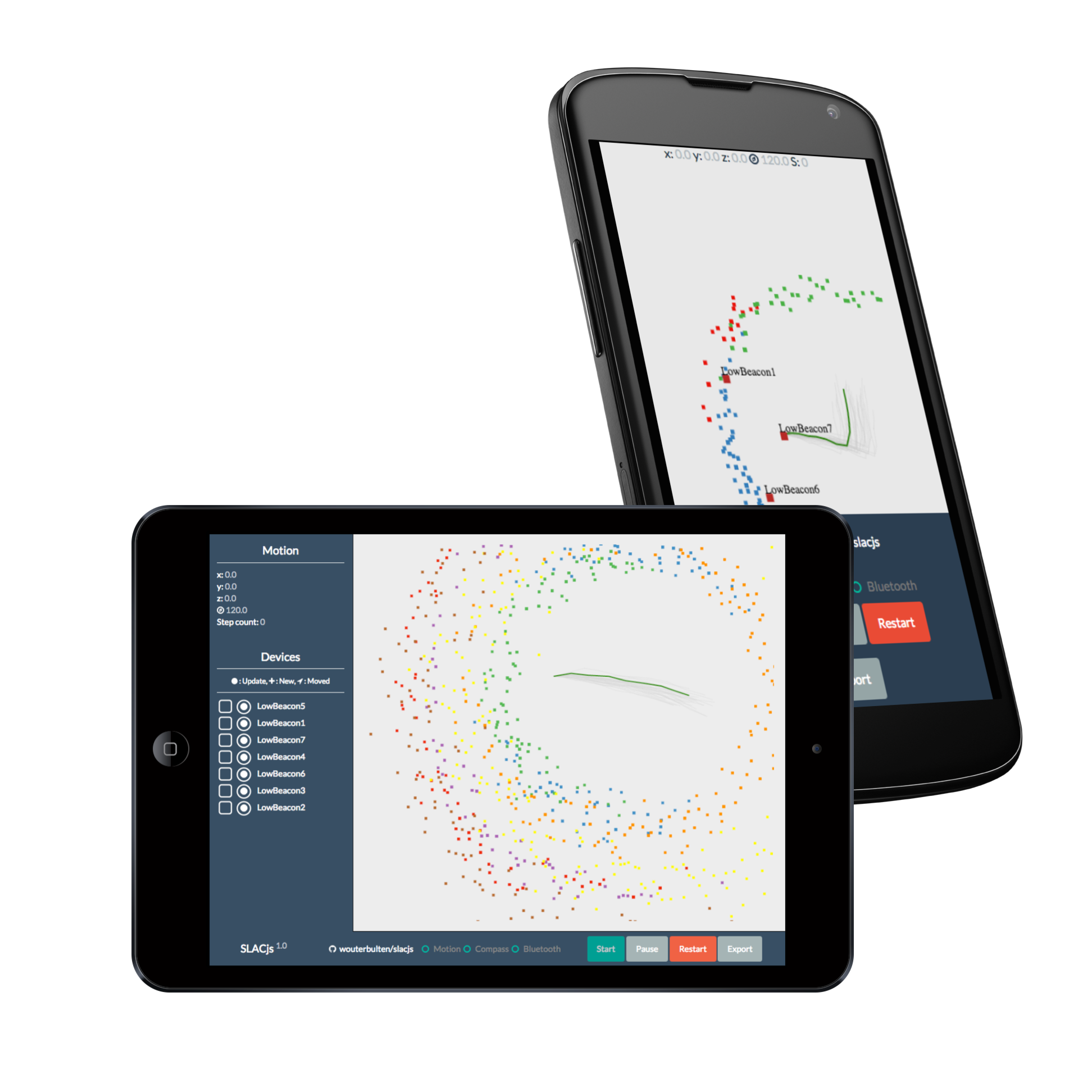
Demo

Average error: ∞ m

Simulations

Perfect world performance

Effect of number of RSSI measurements

Effect of device location


Live tests

Fixed route, average 60 steps / 2 min walking

Effect of environment noise

Effect of RSSI measurements

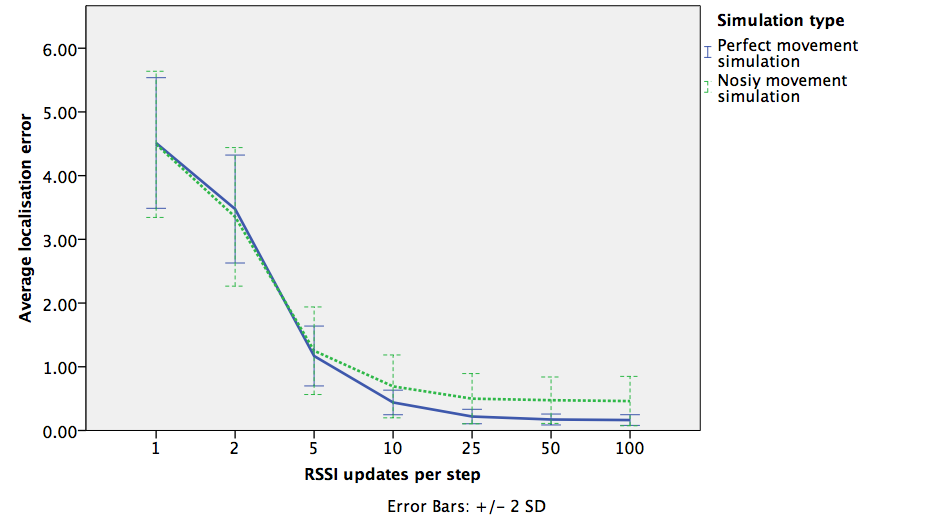Curve estimation model. Significant regression equation.
$$(F (1, 3498) = 33868.750, p < .000), R^2 = .906$$

Effect of device location

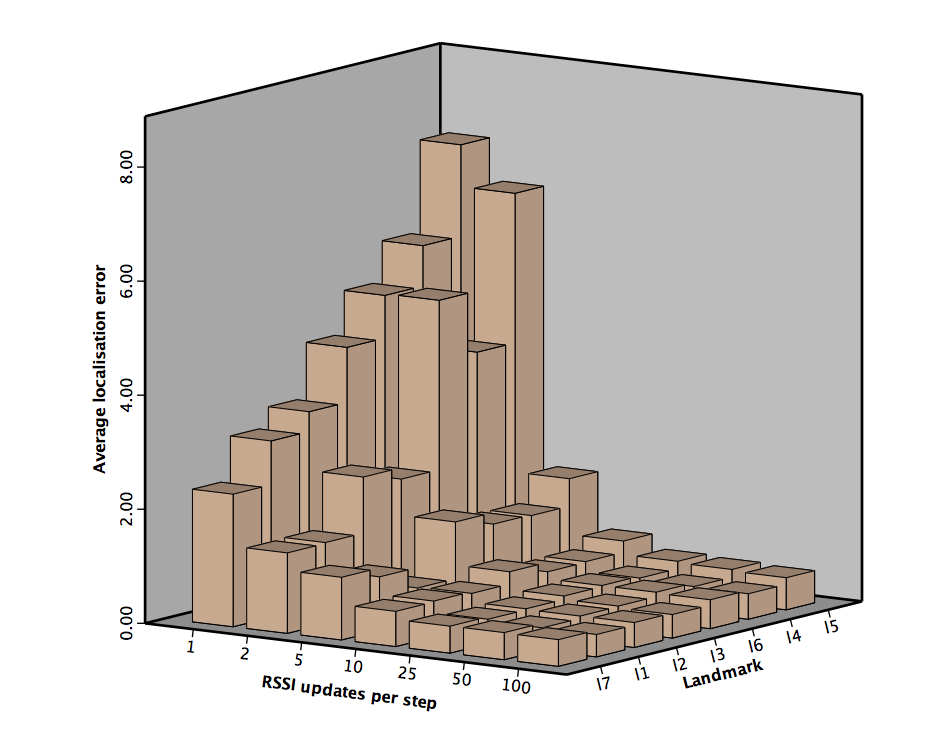Repeated-measure-ANOVA for each condition. Significant effect for each condition (p = .000).
$$eta^2 = [.503, .698, .284, .063, .052, .065, .065]$$

Simulations

Error in meters per landmark, 100 runs per data set

Simulation experiments

Noisy movement: 0.56 m (sd 0.20 m)

Perfect world: 0.26 m (sd 0.07 m)

Zero radio noise     -     Large radio noise

Evaluation method

Online recordings (RSSI & motion)

Offline evaluation, 500 per trace


Measured average localisation error for DoBeacons

97% of runs resulted in estimate for each device

Live tests

Localisation error live tests

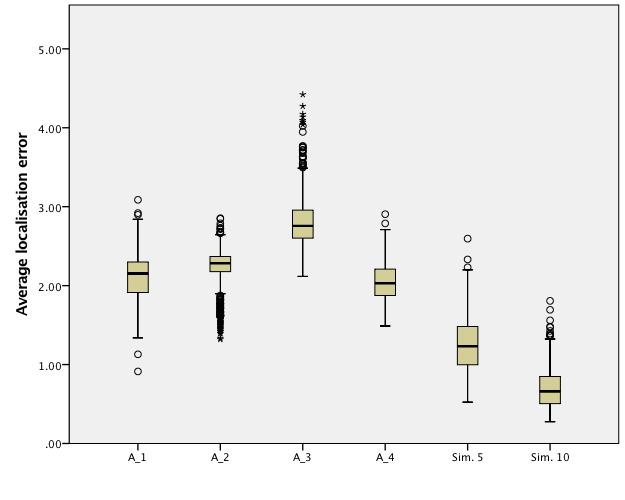
Accuraccy of 2.3m, 60 steps ~ 2min walking

Difference in performance between simulation and real world

Walls, obstacles, users themselves

Mirroring errors


→ Invest in better motion & distance predictions

→ Predict the environment

→ Longer traces

→ Map fusing

Future work: Map fusing

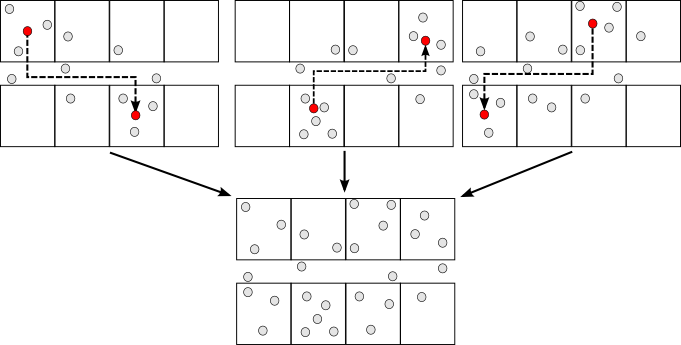
(With respect for user privacy)

“Human SLAM”


Using an adapted range-only version of SLAM, we replaced the robot with a human and used that to locate both humans and devices inside buildings.


Decentralised / Realtime / Without prior information